Способность ставить и решать задачи является одной из базовых для школьной успешности и для самореализации учащегося. Хороший учитель за два-три занятия с классом легко определяет, кто из ребят легко понимает задачи и доводит их решение до конца, кто застревает на середине, кто вообще не умеет с ними справляться. В старших классах мы выделяем в качестве успешных тех учащихся, которые умеют сами поставить задачу в самых разных областях - от задач по освоению дополнительного материала до задач по организации мероприятий в классе. Однако добиться перехода ученика из группы не умеющих решать и ставить задачи в группу умеющих крайне сложно. Чем больше мы объясняем, чем подробнее описываем шаги решения, чем настоятельнее подчеркиваем значимость самостоятельной работы, - тем, как правило, слабее проявляет себя ученик в новой, незнакомой (не «оттренированной» для него) ситуации. Так что же такое задача? Почему успешно решать и ставить задачи может не каждый ребенок? Ответ здесь надо искать в двух областях — в психологии и педагогике.
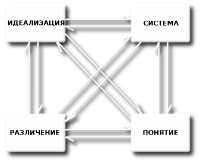
В психологии мышления задача – это инструмент, позволяющий изучать мышление. При решении задач мышление вырабатывает средства и приемы, позволяющие ответить на поставленный вопрос. И задача выступает как определённая форма организации человеком себя для продвижения к поставленной цели с помощью специальных способов. В традиционной педагогической практике задача - средство отработки теоретической части, форма контроля выявления уровня реально освоенного. И в первом и во втором случаях мы имеем дело с мыследеятельностными действиями ученика. Сила психологического подхода - в выявлении средств, имеющихся у ученика, в анализе тех приемов, с помощью которых он начинает работать с исходным материалом для достижения конкретной цели. Сила педагогического подхода - в систематической подборке заданий в рамках одного предмета, в постепенном наращивании их сложности. Метапредмет «Задача» соединяет обе сильные стороны: усложнение системы задач в нем строится по принципу усложнения тех средств работы, которые должны быть освоены учащимся. Мыследеятельностное образование - это образование, построенное на мыследеятельностных принципах и целевым образом сориентированное на формирование мышления, действия, понимания, рефлексии. Результатом такого типа образования являются определенные способности, сформированные на основе присвоения соответствующих способов. В метапредмете «Задача» у учащихся формируются такие способности как: перенос способа решения с одного типа, материала на другой; понимание условий и анализа заданной ситуации; моделирование структур взаимосвязей различных параметров; рефлексивная способность анализа собственного действия; способность изменять подход к пониманию и к способу решения задачи.
Задачи присутствуют во многих учебных предметах (кроме математики, физики, химии, задачи есть и в биологии, географии, русском языке, и уже есть заходы на выстраивание задач в истории и литературе). Есть ли в них что-то общее? С точки зрения предметов, они полностью различны. С точки же зрения анализа средств мышления, мы находим между ними множество интересных связей и соотношений. Метапредмет «Задача» выстраивает особую действительность, в которой рассматриваются нормы и способы, правила и этапы, понятия и варианты решения? Таким образом, мы можем говорить о предмете нового типа - о метапредмете «Задача». Он преподается как самостоятельный предмет. Его целью является обучение школьников решению различных задач. Изучая метапредмет «Задача» учащиеся осваивают обобщенные способы решения различных типов задач в различных предметных дисциплинах.
«Но что есть способ?» - спросите вы. Способ - это то, что должно быть освоено и переведено в персонифицированную форму, в способность. Способ — это устойчивая структура деятельности, закономерная для задач определенного типа1. Описание такой структуры может строиться как на основе использования категории операции, так и на основе использования категории средства. Операционально-алгоритмические системы задания способа не позволяют на единых основаниях сопоставлять способы решения различных типов задач и тем более способы решения задач из разных учебных предметов. Но в мыследеятельностном подходе, ориентированном на выделение средств, такое сопоставление возможно: при решении разного типа задач учащиеся находят (выделяют, порождают, переоткрывают и т.д.) средства, позволяющие сопоставлять различные способы между собой. Например, для простых арифметических задач - оперативные системы (действия сложения, вычитания, умножения, деления) и представления, на основе которых производится перевод выражений текста условий задачи к собственно математически-оперативным2. Для задач на взаимозависимость трех параметров (имеются в виду задачи на движение, работу, стоимость и др.) - средства по составлению уравнения и средства по его решению. Поскольку для решения задачи используется несколько групп средств, то отнесение задачи к тому или иному типу (как и сама типологизация) строится на основе выявления специфических (типообразующих) средств, а также с учетом средств неспецифических для этой и подобных задач. В результате типологизации учащиеся получают возможность «узнавать» задачи одного типа, но разные по материалу, по организации данных, а также отличающиеся постановкой вопроса.
Здесь мы переходим к вопросу как, работая над конкретными задачами, мы можем получить «на ученике» «обобщенное мышление». Имеется в виду мышление, преодолевающее различие задач по сюжету, числовым данным, соотношению величин и т.д. На основе чего это возможно? Первое в ответе на данный вопрос мы уже прояснили: при конструировании учебных задач необходима специальная, логико-дидактическая работа по выделению групп конкретных средств «разбираемой» задачи, которые сами по себе обладают обобщающей характеристикой. Тогда при преподавании оказывается возможным «разворачивание» внимания и действия учащихся на анализ средств, используемых ими при решении соответствующей учебной задачи. Особую обобщающую роль играют вводимые при работе с задачей графические средства: схемы-модели. На них выражаются специфические для данной задачи средства в их числовых или других выражениях.
В метапредмете «Задача» используются также специальные схемы (мы называем их «организационными») для организации прохождения детьми различных этапов решения задачи. Базовая организационная схема, доложенная в основу самого метапредмета, включает шесть этапов работы: первый этап - понимание условий, второй этап - первичная схематизация условий, третий этап - выдвижение идей способа, четвертый этап - моделирование отношений на основании базового специфического средства, пятый этап – осуществление способа/решение, шестой этап* - рефлексивный анализ использованных средств. В рамках каждого из указанных этапов учащиеся осваивают специфические средства деятельности по решению задач. На первом и втором этапах осваиваются средства сюжетного понимания, изоморфного «отражения» (преобразования) выделенных существенных моментов в рисуночно-схемные элементы. На третьем этапе в качестве средств используются знания об имеющихся в опыте отработанных типах задач, алгоритмов и правил их решения: это выражается в том, что учащийся выдвигает предположение, как должна решаться та или другая задача. На четвертом этапе через построение и. последующее использование модели (или без нее) используются средства перевода выделенных существенных данных в математическую форму; в итоге составляется уравнение (математическое выражение). На пятом этапе применяются математические и алгебраические средства решения уравнений, математических выражений.
Что касается шестого этапа, то он не случайно выделен выше звездочкой, так как полностью выбивается из обычной практики работы с задачами. Это происходит по следующей причине: данный этап - замыкающий; в ходе него осуществляется специфическая для метапредмета работа - выделение средств, использованных в процессе решения задачи, т.е. тех средств, с помощью которых и был получен результат. Последний этап построен как учебная задача по обнаружению использованных средств. Это важно, так как смещает внимание учащихся с решения конкретной задачи (нескольких задач), где с получением правильного ответа учебная ситуация собственно и заканчивается, на обнаружение обобщенного средства решения задач определенного типа. Основными средствами на этом этапе являются средства сопоставления, различения производимых решений, моделей, формул и прочих «следов» развернутого мышления при решении нескольких задач с разными сюжетными, числовыми и предметными моментами. В качестве одного из конкретных средств такого сопоставления используется таблица, где в столбцах указаны следующие моменты: текст условий задачи, модельное изображение с нанесёнными данными, полученное уравнение. Для фиксации обнаруженных общих закономерностей используются средства схематических и алгебраических обозначений.
Конструируя новую учебную задачу, преподаватель метапредмета использует набор средств, уже отработанных с предшествующим типом задач смело может на них опираться, попадая в новую учебную ситуацию. В результате такого способа обучения формируются дети, которые не только умеют, любят решать задачи, но и сами оказываются способны конструировать их - в любых предметных областях. Другими словами, они оказываются посвящены в культуру работы с задачами.
1. Алексеев Н.Г. «Рефлексия и формирование способа решения задач»// Диссертация на соискание ученой степени кандидата психологических наук.- М., 2002 (переиздание)
2. Щедровицкий Г.П. «Исследование мышления детей на материале решений простых, арифметических задач»// Развитие познавательных и волевых процессов у дошкольников.- М., 1965